


Up:
2010 and all that
Previous:
Renormalisation
But I've become too serious, hence the preceding unexplained decoration.
When I first wrote on this subject in 1988 with my colleague
Ross Moore,
we began by analysing
John Loxton's monster
and continued by explaining renormalisation.
We concluded by displaying some attractive curlicues--one of which was 2010.
That idea has been refined by
David Angell (from
UNSW)
who supplied me with the pictures shown in this presentation.
More than that, he had the felicitous idea of using the
angle rule 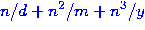 ,
thereby creating a curve for each date
,
thereby creating a curve for each date 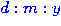 .
This allows one to create designs for individualised birthday cards.
My birthdate is unattractive; I'm jealous of the 10,620 segments of
David's.
.
This allows one to create designs for individualised birthday cards.
My birthdate is unattractive; I'm jealous of the 10,620 segments of
David's.
Other rules are possible;
the next examples include things like 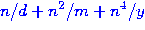 or
or 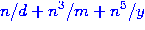 and changing the order of the powers of
and changing the order of the powers of  .
.
(Click images for a larger version.)
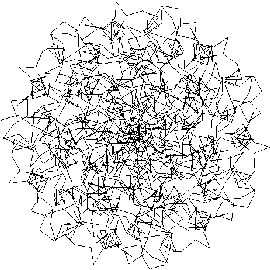
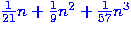
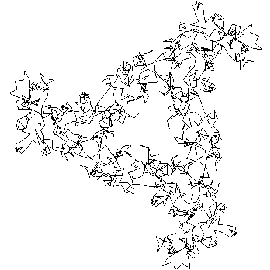
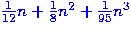

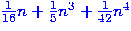

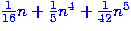
 Christmas 1994:
Christmas 1994: 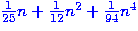
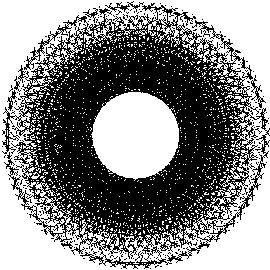 ...more good tidings:
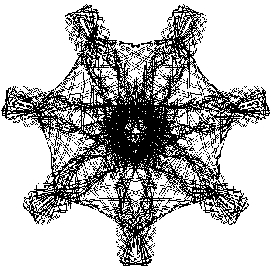
...more good tidings: 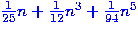
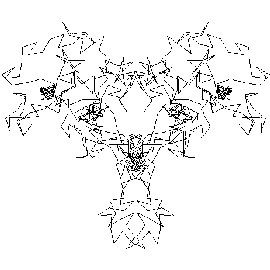
Here are some more examples using different formulæ.
The variability attainable in the nature of the curves is quite striking.
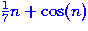
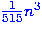

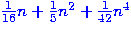



Up:
2010 and all that
Previous:
Renormalisation
Ross Moore ross@ics.mq.edu.au
1/28/1997

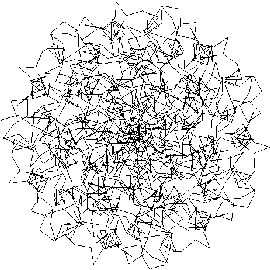



 Christmas 1994:
Christmas 1994:  ...more good tidings:
...more good tidings: 
